La Circunferencia es una línea curva cerrada y plana, en la cual todos los puntos de dicha línea están a la misma distancia de un punto central llamado Centro.
El Círculo es el espacio o superficie que hay dentro de una circunferencia.
La Circunferencia es una línea mientras que el Círculo es una superficie.
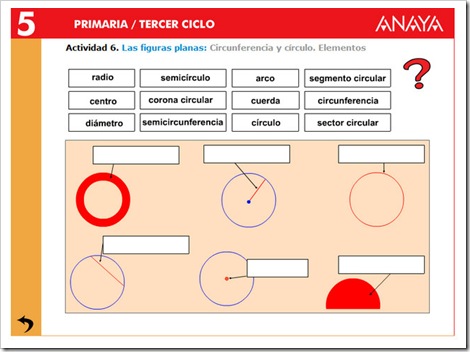
Elementos de la Circunferencia
En la Circunferencia hay elementos singulares que veremos a continuación.
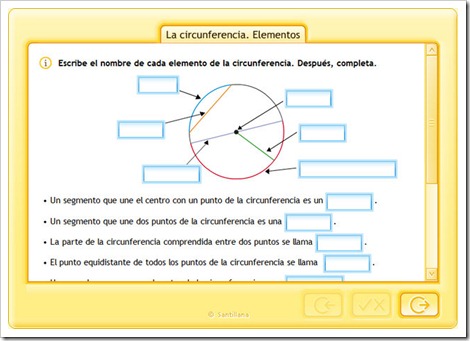
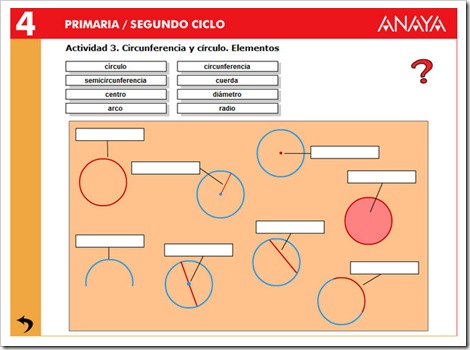
Centro ⇒ Punto interior que equidista de todos los puntos de la circunferencia.
Radio ⇒ Segmento que une el centro con un punto cualquiera de la circunferencia.
Diámetro ⇒ Segmento que une dos puntos de la circunferencia pasando por el centro.
Cuerda ⇒ Segmento que une dos puntos de la circunferencia sin pasar por el centro.
Secante ⇒ Recta que corta a la circunferencia en dos puntos.
Tangente ⇒ Recta que toca a la circunferencia en un sólo punto.
Arco ⇒ Segmento curvilíneo entre dos puntos pertenecientes a la circunferencia.
Elementos del Círculo
La definición dada para los elementos y los ángulos de la circunferencia es aplicable al círculo al ser la circunferencia parte del círculo. La Circunferencia es el Perímetro del Círculo.
El círculo, al ser una figura plana, tiene unos Elementos Propios que veremos a continuación.
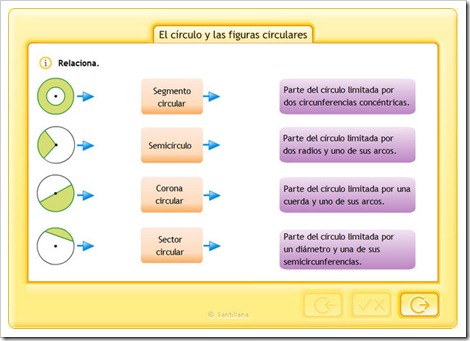
Semicírculo ⇒ Porción de círculo limitada por un diámetro y su arco correspondiente. Equivale a la mitad del círculo.Área → Asemicirculo = (π r2) / 2 | ||
Sector circular ⇒ Porción de círculo limitada por dos radios y su arco correspondiente. (ߺ = valor del ángulo).Área → Asector = π r2 ߺ / 360º | ||
Segmento circular ⇒ Parte del círculo limitada por una cuerda y su arco. (ߺ = valor del ángulo)Área → Asegmento = r2 (ߺ - sen ߺ) / 2 | ||
Corona circular ⇒ Porción de círculo limitada por dos circunferencias concéntricas. (R = radio mayor, r = radio menor)Área → Acorona = π (R2 - r2) | ||
Trapecio circular ⇒ Porción de círculo limitada por dos radios y una corona circular. (R = radio mayor, r = radio menor, ߺ = valor del ángulo)Área → Atrapecio = π (R2 - r2) ߺ / 360º | ||

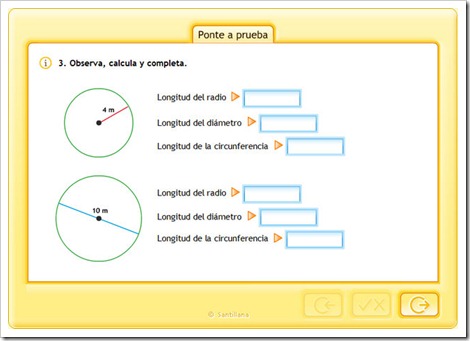
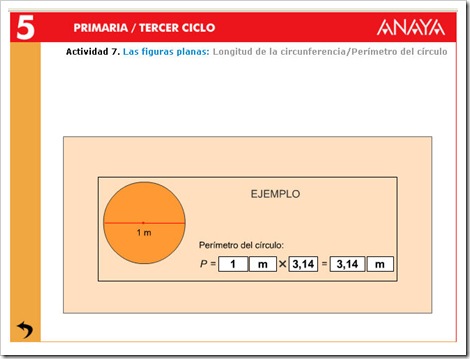
La longitud de la circunferencia







No hay comentarios:
Publicar un comentario